AGC Research Report 75(2025)
アルミノケイ酸塩ガラスの格子熱伝導率と組成依存性
Thermal Conductivity of Aluminosilicate Glasses and Its Compositional Dependence
門 力也*
Rikiya Kado
*AGC株式会社 材料融合研究所(rikiya.kado@agc.com)
ガラスの格子熱伝導の制御に向けて、その組成依存性を理解することは不可欠である。本研究では、比較的熱伝導率の高いアルミノケイ酸塩ガラス系について格子熱伝導率を評価し、既往の熱伝導率推定式を検証するとともに拡散熱伝導モデルに基づいて組成依存性を考察した。アルカリ土類混合系において熱伝導率は非線形な組成依存性を示したが、これは混合効果が主要因ではなく、高熱伝導ガラス特有の挙動と示唆された。また、拡散熱伝導モデルによる解析の結果、そのようなガラスでは拡散モード(diffusons)よりも伝搬モード(propagons)による寄与が大きい傾向にあり、これが熱伝導率の推定値と実測値との乖離要因になることが示唆された。
Understanding how lattice thermal conductivity depends on composition is crucial for managing thermal transport in glass. This study evaluated the lattice thermal conductivity of aluminosilicate glass systems, which are known for their relatively high thermal conductivity, and assessed the validity of existing empirical models for thermal conductivity in glasses. The study also analyzed the compositional dependence using the diffusional thermal conductivity model. In alkali-earth mixed systems, thermal conductivity showed a non-linear relationship with composition. This behavior does not seem to be primarily caused by mixing effects but instead reflects the inherent characteristics of high thermal conductivity glasses. In addition, analysis via the diffusional thermal conductivity model indicated that the contribution from propagating modes(propagons)tends to be greater than that from diffusive modes(diffusons)in these glasses. This distinction may help explain the discrepancies observed between estimated and experimentally measured thermal conductivity values.
1. 緒言
材料による格子熱伝導の制御は古くから重要な研究対象(1)であるが、高熱伝導率化(2)、低熱伝導率化(3,4)問わず、その制御は近年ますます重要になっている。ガラスの熱伝導率は、構造的な乱雑さに起因する平均自由行程の短さから無機化合物の結晶と比較して数桁小さい(6,7)が、有機物の代表的透明材料であるアクリル樹脂と比べれば高い。また、他の透明材料と比較して光透過性や耐熱性、成形性に優れることから、熱伝導率を向上させることができれば、プロジェクターレンズや自動車用ヘッドライト部材といった既存の用途に高い放熱性を持たせることができる。さらに、半導体パッケージ基板やLED基板など、新規の応用先へも展開が期待される。また、半導体用キャリア基板ガラスなど、ホットプレート上で熱処理が行われる材料においては熱反りを低減するために熱伝導率の高い材料が求められる。一般的にガラスの室温における熱伝導率は0.3〜1.0 W/(m・K)程度であるが、 SiO2ガラスはおおよそ1.5 W/(m・K)と比較的高く、さらに結晶化ガラスではそれを超える熱伝導率付与が可能である(8)。しかし、いずれも製造が容易ではなく加工が難しい材料であり、かつキャリア基板では熱膨張率やヤング率、光学用ガラスであれば屈折率や透過率などの他の特性と合わせた高熱伝導率の設計が必要とされる。したがって、ガラスの熱伝導率を設計する上で、その組成依存性を理解することは重要となる。
ガラスの熱伝導率の組成依存性に関する研究例の一つとして、稲葉らによって様々なガラス組成系に適用可能な熱伝導率の推定式が提案されている(9)。この式では、ガラスを構成する酸化物成分の比率と密度の情報のみから、室温における熱伝導率を計算することができる。ガラス系に依らず幅広い組成に対して熱伝導率の計算が可能であるが、熱伝導率が0.9 W/(m・K)を超える領域では予測精度が著しく低下するという問題がある。この要因は、本推定式における平均自由行程の近似方法で、長い平均自由行程を有するガラス系には適応できないと結論付けている。松岡ら(10,11)は熱伝導率に関する基盤研究において、ガラスの熱伝導率の組成依存性は平均自由行程と相関性があると述べている。また、混合アルカリケイ酸塩ガラスの熱伝導率を系統的に測定し、熱伝導率および平均自由行程において混合アルカリ効果を観測している。アルミノケイ酸塩ガラス:33Na2O–xAlO3/2–(67-x) SiO2とホウケイ酸塩ガラス:yNa2O–1.0B2O3–1.0SiO2では、Al、Bの配位数変化によってガラス構造中の非架橋酸素比率が変化する。非架橋酸素の比率によって平均自由行程が変化することが熱伝導率の組成依存性が認められる原因と考察している(7,11)。最近の文献でも、Li2O–B2O3系にて4配位ホウ素の割合に対して熱伝導率が線形に変化することが示されている(12)。このように、単純組成系に関する熱伝導率の組成依存性はいくつか調査されており、ケイ酸塩ガラスとホウ酸塩ガラスの比較のような大きな構造的差異による効果の解釈はなされているものの、組成依存性に関する定量的な理解や広い組成系に対する一般化は達成できていない。また、実用的な組成系を調査した文献は限られており(13)、特に高熱伝導率領域の理解は不十分である。
上述した一連の報告では、ガラス構造中でもフォノンの伝搬とその平均自由行程を定義して議論が行われていることが多い。格子熱伝導をフォノン伝搬のみで説明しないアモルファス材料における熱伝導モデルとして、熱伝導タイプをpropagonsとdiffusons、loconsの3つのカテゴリに分類したAllenとFeldmanによるモデルが提案されている(14,15)。このモデルでは、 propagonsとdiffusonsが主たる熱輸送因子であり、 loconsは他の伝導モードへの相互作用でのみ影響を及ぼす。propagonsは従来のフォノンの伝搬に似た定義可能な波数ベクトルを持つ振動モードであり、 diffusonsは定義可能な波数ベクトルを持たない熱拡散モードである(Fig. 1(16))。一般的に、高剛性で欠陥の少ない結晶性固体ではpropagonsの寄与が支配的であるのに対して、非結晶性の低剛性固体では、 diffusonsが支配的な傾向にあるという。Agneらは、実験事実に基づく経験式を用いてAllenとFeldmanの熱伝導モデルを簡略化し、新たなモデルを提案した(16)。本モデルでは実験的に求めた平均音速から熱拡散モードdiffusonsの熱伝導への寄与を算出することができる。Sørensenらは、Agneらによって提唱されたモデルをガラス材料に適用し、ガラス組成系と熱伝導モードの関係性を調査した(17,18)。2成分系のアルカリケイ酸塩ガラスとアルカリホウ酸塩ガラスにおける拡散熱伝導モード(diffusons)を計算すると、ホウ酸塩ガラス中の熱伝導はdiffusonsが支配的であるのに対して、シリケートガラス中ではdiffusonsと propagonsの両方が寄与していることが報告されている(17)。この違いはガラスの構造的特徴で解釈されている。ガラス中でケイ素は4配位でのみ存在しているが、ホウ素は3配位と4配位を取るため、この配位数分布がフォノ ン(propagons) を散乱さ せ、 propagonsの伝搬が制限されていると説明付けている。このように、熱伝導因子をdiffusonsとpropagons(とlocons)に分類したモデルを適用することによって、ガラスの熱伝導率と組成、構造の関係の理解を深めることができる。さらに、上述した熱伝導率の推定式によって計算された熱伝導率と実測値の差を説明する手掛かりになる可能性がある。
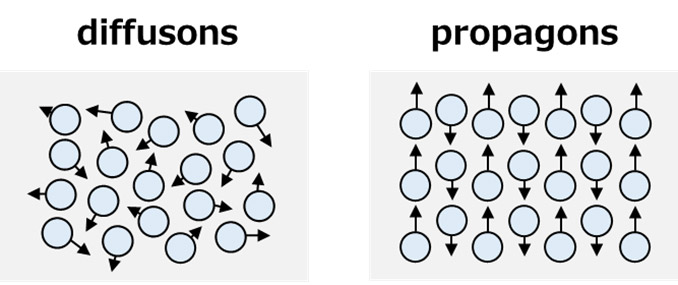 Fig. 1 Schematic of diffusons and propagons in atoms.
Fig. 1 Schematic of diffusons and propagons in atoms.本研究では、比較的高熱伝導を示すガラス組成系であるアルミノケイ酸塩ガラス系に対して、熱伝導率の評価および上述したモデル解析を行い、高熱伝導領域において半経験式による熱伝導率の予測誤差が大きくなる要因について理解を深めることを目的とする。
2. 実験方法
2.1. ガラス作製
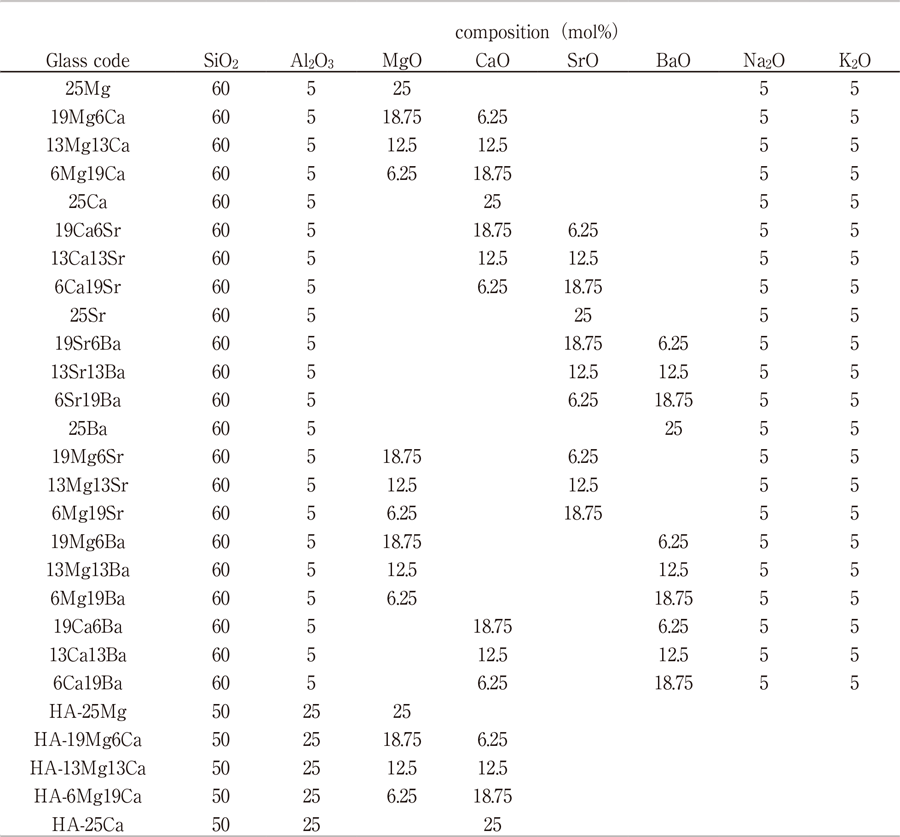
本研究で用いたガラス組成をTable 1に示す。アルカリ土類Mg, Ca, Sr, Baの4種のうち2種類を混合した組成を準備した。熱伝導率の大きさを変えるために、 Al2O3含有量の異なる2種類(低アルミナ系:Al2O3 5mol%、高アルミナ系:Al2O3 25 mol%)の組成系を用意した。これらのガラスは溶融急冷法によって作製された。得られるガラス量が700 gとなるように工業原料グレードのSiO2、Al2O3、Na2CO3、CaCO3、 MgOおよび清澄剤を所定量秤量した後、乾式混合して原料バッチとした。原料バッチを白金るつぼに入れ、1773 K〜1923 Kの大気雰囲気中で1時間溶融し、カーボン板上にキャストした。キャスト直後にガラスを水砕し、再度撹拌しながら2時間溶融することで均質なガラス融液を得た。得られたガラス融液を予熱したカーボン板上に再度キャストして固化させた後、直ちに徐冷炉に投入し、ガラス転移温度+30 Kで1時間保持後、1 K/minで室温まで降温してガラスブロックを得た。得られたガラスブロックを切断・研磨することで各物性測定用の所望のサンプルを得た。
2.2. 熱伝導率及び諸物性の評価
ガラス転移温度Tg[K]の測定には、NETZSCH製の熱膨張計DIL402 Expedisを用いた。測定には、各ガラスをφ6 mm×25 mmの円柱状に加工したサンプルを用いた。
熱伝導率は密度ρ[kg/m3]、比熱CP[ J/(g・K)]、熱拡散率α[10-6・m2/s]を用いて、熱拡散率の定義式(1)より算出した。以下にそれぞれの物性の測定方法を示す。
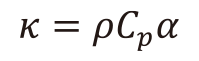 (1)
(1)密度は、METTLERTOLEDO製の電子天秤XPE105を用い、アルキメデス法にて測定した。測定には、一辺10 mm程度の直方体サンプルを用いた。
比熱の測定は、NETZSCH製の示差走査熱量測定装置DSC404F3を用いて、昇温速度5K/minで室温から673Kまで行った。測定には、各ガラスをφ6 mm×0.5 mmの円盤状に加工し、上下面を鏡面研磨したサンプルを用いた。各試料の測定の前に、ベースライン測定として空のPtパン、リファレンス測定として比熱が既知のサファイアディスクの測定を、試料の測定と同じ温度プロファイルで行った。CPの算出はDIN51007規格に基づき、室温保持と高温保持におけるベースラインのドリフト補正を行った。
熱拡散率は京都電子工業製のレーザーフラッシュ法測定装置LFA-502を用いて室温から673 Kまで100 Kごとに測定した。測定には、各ガラスをφ5 mm×1mmの円盤状に加工したサンプルを用いた。試料面における温度応答は熱拡散方程式より、
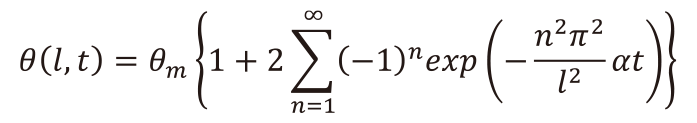 (2)
(2)と表すことができる。ここで、θは試料裏面の応答温度、θmは応答温度の最高値、l は試料の厚さ、αは試料の熱拡散率、tは時間である。熱拡散率はハーフタイム法により算出した。一般的に、θ/θm=0.5となる時間τ1/2を用いて熱拡散率は、
 (3)
(3)と表すことができる。平均音速υS[m/s]およびヤング 率E[GPa]の測定には、超音波パルス法(OLYMPUS社製38DL PLUS)を用いた。縦波速度 υLと横波速度υTを測定し、次式よりそれぞれ算出した。
 (5)
(5)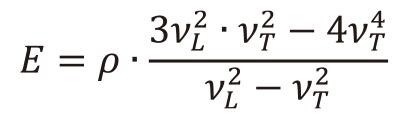 (6)
(6)ここで、ρは密度[kg/m3]を表しており、アルキメデス法で実測した値を用いた。測定には、30 mm×30 mm×1 mmの平板サンプルを用いた。
2.3. 熱伝導率の計算
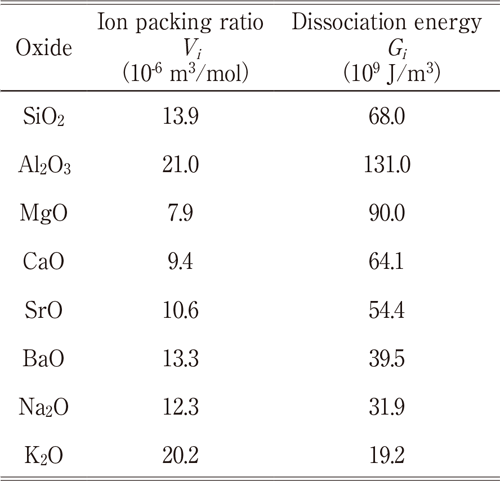
稲葉らの文献(9)に基づいて、室温の熱伝導率及び関連する物性値を、組成から計算されるパラメータ及び室温における実測密度を用いて計算した。本研究では、パラメータの計算にはTable 2(9)に記載の値を用いた。以下、その概要を記す。
熱拡散率α[m2/s]は、ガラスの熱伝達をフォノンの拡散としてとらえれば、気体分子運動論より平均音速υSと平均自由行程 l[m]を用いて、次式で表すことができる。
 (7)
(7)このうち平均音速υSは√E/ρに比例することが知られており、酸化物ガラスについては以下の(8)式で表せられる。
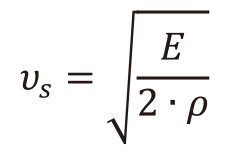 (8)
(8)さらに、酸化物ガラスのヤング率Eは、イオン充填率Vp[m3/mol]と解離エネルギーGt[J/m3]を用いて次式より推定することができる(19)。
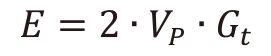 (9)
(9)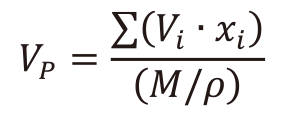 (10)
(10)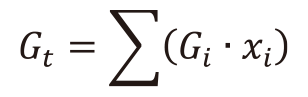 (11)
(11)イオン充填率Vpの式中のMは平均分子量[g/mol]であり、xiは組成比[mol%]である。またVi及びGiは各ガラスを構成する酸化物i に対して求まる組成パラメータである。
以上より、酸化物ガラスの平均音速υSと組成の関係は次式より評価できる。
 (12)
(12)また、室温付近の平均自由行程はフォノンの波長に等しいとする理論に従い、ガラスの平均自由行程を計算できる。ただし、ここでは平均自由行程がフォノンの最短波長λmin[nm]で与えられるとし、(13)式から推算している。
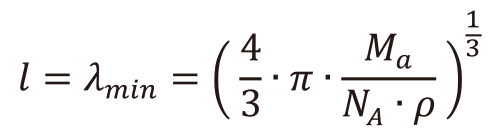 (13)
(13)ここで、Mαは平均原子量[g/mol]、NAはアボガドロ定数[mol-1]である。(7)式に(12)式及び(13)式を代入することで、熱拡散率の推定式(14)を得る。
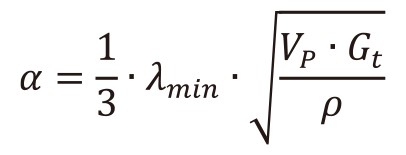 (14)
(14)比熱CPの算出にはデバイ温度Θ[K]における比熱CPΘ[J/(g・K)]を用いている。比熱、温度を、それぞれデバイ温度における比熱CPΘ、デバイ温度Θで規格化することで組成に依らず1つの曲線で近似できる。この時の近似曲線を次式(15)で示す。
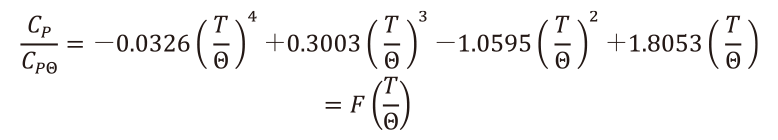 (15)
(15)このうちデバイ温度は、ガラス中を伝搬するフォノンの最大振動数が、デバイモデルにおける振動数の上限を与えるとすれば、以下の(16)式で表すことができる。
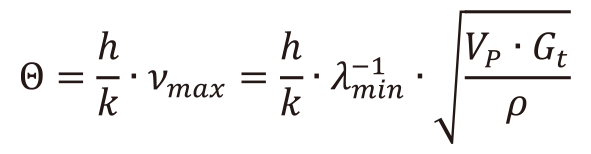 (16)
(16)また、規格化した比熱CP/CPΘが十分高温では1.3近傍に漸近することと、ガラスの比熱がデュロンープティの法則に従い3R /Mαに収束することを仮定すれば、デバイ温度における比熱は次式により求めることができる。
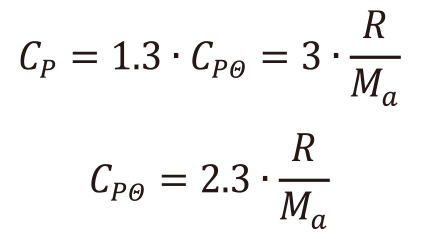 (17)
(17)ここで、R は気体定数[J/(mol・K)]である。
式(15)及び式(17)から、比熱推定式(18)を導くことができる。
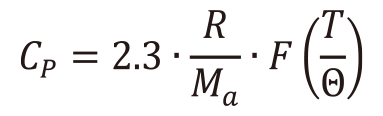 (18)
(18)式(14)の熱拡散率推定式及び式(18)の比熱推定式と実測密度ρを用いて(1)式より熱伝導率推定式として次式が得られる。
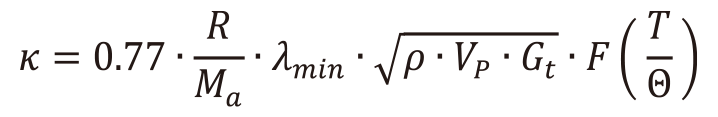 (19)
(19)
2.4. 拡散熱伝導率(κdiff)の計算
固体の原子振動によって運ばれる熱伝導率のモデルでは、熱伝導率は次の3つの因子で表される(20)式)。(i)熱を運ぶために利用できる特定のエネルギーの振動数、つまり振動状態の振動密度、g(ω)、(ii)各振動によって運ばれる熱量、つまりモードごとの熱容量、C(ω)、(iii)これらの振動の伝播挙動、つまり各振動の熱拡散率D(ω)。
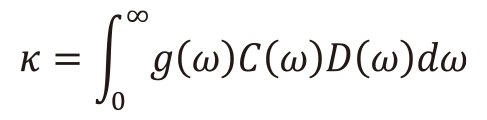 (20)
(20)詳細は割愛するが、Bose-Einstein統計から導き出される格子振動の熱容量C(ω)と、ランダムウォーク理論に基づくAllen-Feldmanの拡散理論によって導かれる熱拡散率κdiff(ω)を用いることで(14,16,20)を参照)、diffusonsの最大熱伝導率κdiffは系の状態密度 g(ω)のみで表すことができる。
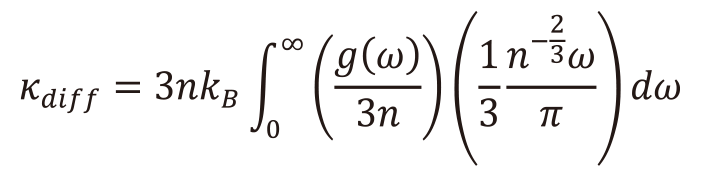 (21)
(21)このモデルでは、各振動子(diffusons)はお互いに完全に独立しており、群速度と緩和時間によって定義されるフォノンの伝搬とは根本的に異なる輸送の形態をもつ。本モデルの妥当性は非晶質シリコンのMD計算(14)と実測値(16,21)との比較から検証されている。
多くの場合、状態密度 g(ω)を実験的または計算的に知ることは困難であることから、本モデルでは2つの経験式を用いることで拡散熱伝導率κdiffの計算式を簡略化している。最終的にκdiffは(22)式のように原子の数密度nと音速νT、νLのみで表すことができる。
 (22)
(22)デバイ温度以下では熱的に励起されていない振動があるため、κdiffの温度依存性を考慮すると、κdiff(T)は(23)式で与えられる。
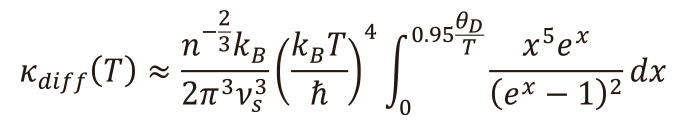 (23)
(23)3. 実験結果
3.1. 各種物性評価結果
Table 3に本研究で作製したガラスの各種物性値を示す。ここで、比熱、熱拡散率、熱伝導率は室温の値である。物性によっては複数回測定しており、装置精度と合わせた標準誤差はそれぞれ、密度は±0.1%以下、比熱は約±3%、熱拡散率は±1%以下、熱伝導率は約±5%以下、ヤング率は約±1%と見積もられた。含有しているアルカリ土類金属の種類・比率に依存して、物性値に大きな変化がみられた。熱伝導率κは0.65〜1.41[W/(m・K)]と広く分布しており、HA-25Mgの熱伝導率κ=1.41[W/(m・K)]は、 SiO2ガラスの値κ=1.47[W/(m・K)]に匹敵した。
3.2. ガラス転移温度に与える混合アルカリ土類効果の影響
Fig. 2にガラス転移温度のアルカリ土類混合比に対する変化を示す。ここで、横軸はアルカリ土類金属酸化物の総含有量における任意の1種のアルカリ土類金属酸化物の含有量の割合(R’O/(RO+R’O)、R, R’ =Mg, Ca, Sr,Ba)を示す。Fig. 2に示すように、ガラス転移温度はどの混合系においても非線形な組成依存性を示し、アルカリ土類金属の置換率によってガラス転移温度は減少した。Mg/Ca混合系では、MgイオンとCaイオンの濃度が等しい組成(CaO/(MgO+CaO)=0.5)に近い領域で最大の混合アルカリ土類効果が確認されたが、置換するイオンのサイズが大きくなるにつれて、混合効果が最大となる組成は置換率の高い(1に近い)側にシフトした(Fig. 2(a))。非線形な混合効果はMg/Ca混合系における粘性に関連する特性(ガラス転移温度(22)、フラジリティ(22)、軟化点(23)、高温粘性(24))で報告されており、本研究ではSrやBaを含むアルカリ土類混合系でも同様の非線形な物性変化が確認された。混合による非線形応答の要因として、混合によって引き起こされる過剰エントロピーの増大(24)や異種カチオンによる酸素イオンの安定化(25)が唱えられているが、Kjeldsenら(22)の系統的な調査では、後者の仮説は実験結果とは正反対のことを示していると説明されている。
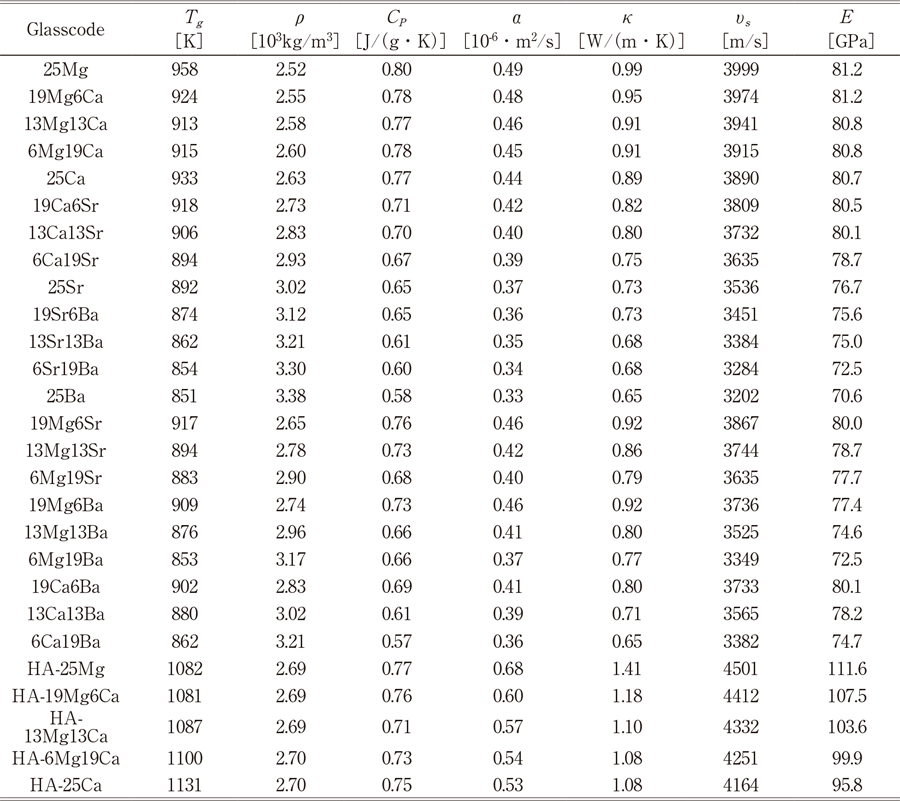
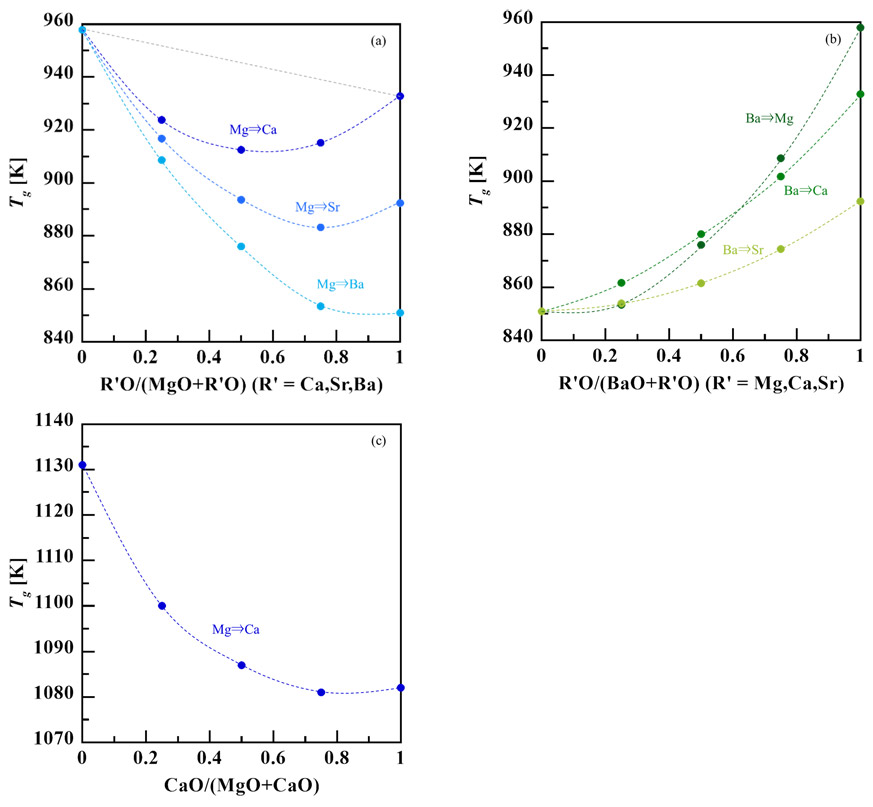 Fig. 2 Glass transition temperature as a function of the molar ratio of a certain alkaline earth to total alkaline earth content. (a) Mg is substituted by other alkaline earths in low Al2O3 system, (b) Ba is substituted by other alkaline earths in low Al2O3 system, (c) High Al2O3 system. Dash lines represent the apparent relations. Gray dash line represents linear relation.
Fig. 2 Glass transition temperature as a function of the molar ratio of a certain alkaline earth to total alkaline earth content. (a) Mg is substituted by other alkaline earths in low Al2O3 system, (b) Ba is substituted by other alkaline earths in low Al2O3 system, (c) High Al2O3 system. Dash lines represent the apparent relations. Gray dash line represents linear relation.3.3. 熱伝導率の組成依存性
Fig. 3にアルカリ土類混合比に対する熱伝導率の変化を示す。熱伝導率でも組成系によって異なる依存性が確認されたが、アルカリ土類種による違いはなく、低アルミナ系と高アルミナ系で異なる傾向がみられた。低アルミナ系(Fig. 3(a)ではいずれの混合系でも線形な組成依存性が確認されたが、Fig. 3(b)に示すように高アルミナ系では顕著な非線形応答が確認された。Fig. 4にMg/Ca系について低アルミナ系と高アルミナ系を比較した結果を示す。Mg⇒Ca置換に対する応答は明瞭に異なっており、CaOを含まない高アルミナ系ガラスでは、混合効果以外に熱伝導率を高める効果が働いていることを示唆している。
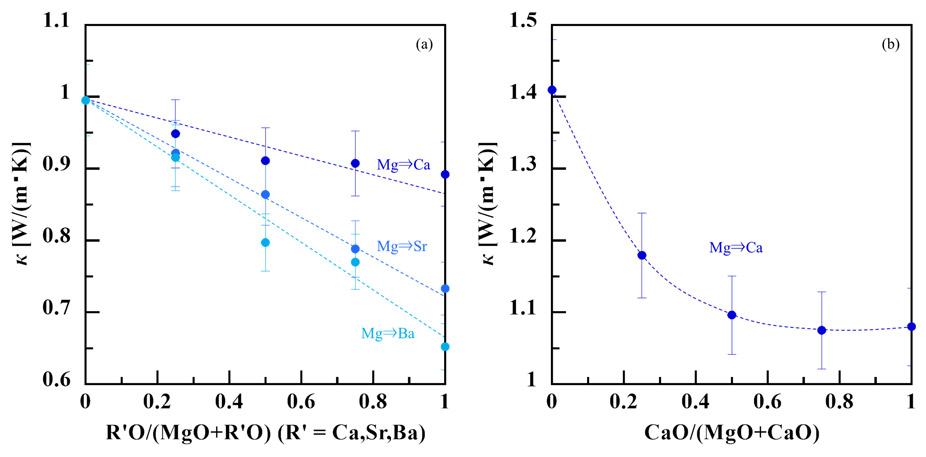 Fig. 3 Thermal conductivity of Mg/Ca mixed systems.(a) κ in low Al2O3 system,(b)κ in high Al2O3 system. Dash lines represent the apparent relations.
Fig. 3 Thermal conductivity of Mg/Ca mixed systems.(a) κ in low Al2O3 system,(b)κ in high Al2O3 system. Dash lines represent the apparent relations.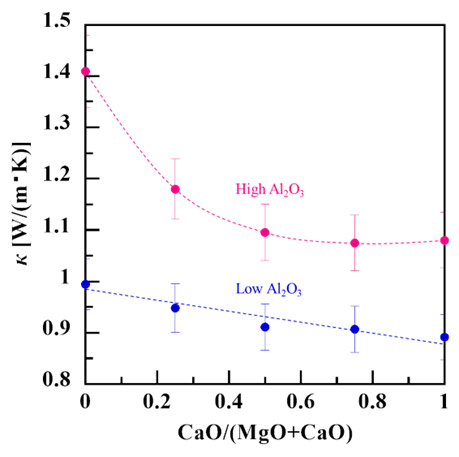 Fig. 4 Comparison of thermal conductivity with CaO/(MgO + CaO)in low Al2O3 system and high Al2O3 system. Dash line of low Al2O3 system represents the linear fit, and that of high Al2O3 system represents the apparent relation.
Fig. 4 Comparison of thermal conductivity with CaO/(MgO + CaO)in low Al2O3 system and high Al2O3 system. Dash line of low Al2O3 system represents the linear fit, and that of high Al2O3 system represents the apparent relation.3.4. 半経験式による熱伝導率の計算結果
Fig. 5に熱伝導率推定式による計算値κcalと実測値κの比較を示す。実測値κは0.65〜1.41[W/(m・K)]と広い分布を示すのに対して、計算値κcalの分布は0.79〜0.98[W/(m・K)]であった。前述した既報と同様に、おおよそ0.9[W/(m・K)]を超える領域では計算値と実測値の乖離が大きくなる傾向を示した。また、低熱伝導率側では計算値よりも実測値が小さくなる傾向を示した。
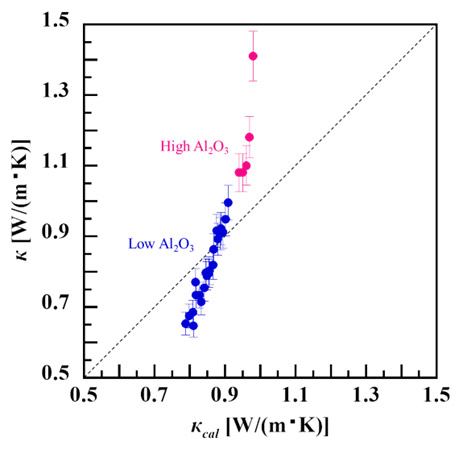 Fig. 5
Fig. 5Fig. 5 Comparison of calculated and measured values of thermal conductivity. Blue plots: low Al2O3 system, pink plots: high Al2O3 system. Dash lines represent κ = κcal.
3.5. 拡散熱伝導率κの計算結果
Fig. 6に拡散熱伝導モデルにより算出したκdiff及び格子熱伝導率の実測値κを示す。ここでは、文献(18)と同様に横軸には平均音速υsを用いている。この結果は、ケイ酸塩系、ホウ酸塩系の報告(17,18)および、14種類のカルコゲナイドガラスとその縦波速度について報告された傾向(25)とも一致している。平均音速が増加すると熱伝導率κは増加する傾向であるが、その増加率も増大しており、おおよそκ=0.9[W/(m・K)]を境にdiffusonsの熱伝導率κdiffの寄与が変わっているようにみえる。低熱伝導(低平均音速)領域では格子熱伝導率κに対するκdiffの寄与が大きいが、熱伝導率が高くなる(平均音速が大きくなる)につれてκdiffの寄与が相対的に下がっている。
 Fig. 6 Measured thermal conductivity κ(solid circles)and contribution of diffusons to thermal conductivity κdiff(solid squares)as a function of average sound speed for studied glasses.
Fig. 6 Measured thermal conductivity κ(solid circles)and contribution of diffusons to thermal conductivity κdiff(solid squares)as a function of average sound speed for studied glasses.4. 考察
4.1. フォノンの平均自由行程既報の文献(9)では、高熱伝導率を有するガラス組成において格子熱伝導率の計算値と実測値が大きく乖離する要因は、平均自由行程が長い高熱伝導率ガラスでフォノンの最短波長λminによる平均自由行程lの近似が適切でなくなることだと述べている。これまで述べたように、非晶質材料の主たる熱伝導をフォノン伝搬モデルで定義することの蓋然性は不確かであるが、本研究で用いた組成系について算出した平均自由行程の変化について述べておく。
Fig. 7に、(7)式を用いて平均音速と熱拡散率から求めたフォノンの平均自由行程を示す。実験値と計算値から求めた平均自由行程を比較したところ、計算値の組成依存性は乏しく、実験値との間にはわずかな負の相関が見られた。(13)式によれば、平均自由行程の計算値は平均原子容の1/3乗に比例する。しかし、本研究における実測値は、これとは逆に原子容に対して負の相関を示した(Fig. 7)。この関係を考察するために、まず一般的なシリケートガラスの例を挙げる。シリケートガラスでは、修飾酸化物の含有量を増やすと密度の増加に伴い平均原子容が小さくなる。この場合、修飾イオンがガラス骨格を切断するためフォノンの散乱が増大し、実測の平均自由行程は短くなる。計算値も平均原子容の減少に応じて短くなるため、この例では計算値と実測値は正の相関を持つ。次に、本研究の低アルミナ系に注目すると、修飾酸化物であるアルカリ土類酸化物の総含有量は、組成によらず一定である。その中で、SrやBaと比較してイオン半径の小さいMgやCaを含有する組成ほど、平均原子容が小さい傾向が見られた。この系で実測の平均自由行程が平均原子容と負の相関を示した要因として、以下のことが考えられる。MgやCaのようなイオン半径の小さい修飾イオンは、ネットワークを形成するSiやAlとのイオン半径の差が比較的小さくなる。そのため、ガラスネットワーク全体の結合距離など構造的な分布の揺らぎが抑制されると想定される。その結果、SrやBaを含有する平均原子容の大きい構造に比べてフォノンの散乱が弱まり、平均自由行程が長くなったと考えられる。
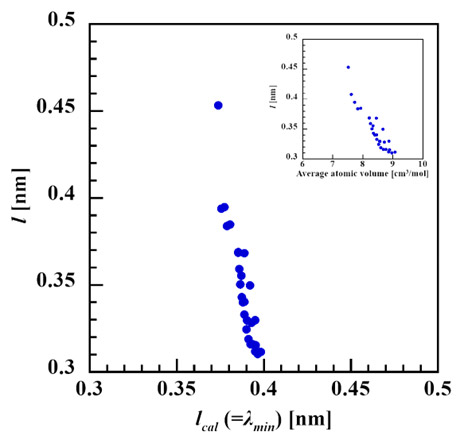 Fig. 7 Phonon mean free path compared with calculated value(=λmin). The inset shows correlation between average atomic volume and phonon mean free path.
Fig. 7 Phonon mean free path compared with calculated value(=λmin). The inset shows correlation between average atomic volume and phonon mean free path.4.2. Al配位数と熱伝導率
従来のフォノン伝搬のような熱伝導を考えた場合、平均自由行程は0.3〜0.5nm程度と見積もられる。 Na2O-Al2O3-SiO2系ガラス中のSi-O間距離が約0.16 nm(26,27)、Al-O間距離が約0.18 nm(28)、Na-O間距離が0.22〜0.24 nm(27)であることから、フォノンの平均自由行程はガラス中のカチオン-酸素結合2〜3個相当の長さである。すなわち、いわゆるシリケートネットワークにおけるQn分布のような近距離秩序も影響を与える可能性がある(非架橋酸素の生成やNa-Oの生成によって、熱振動の局在化が生じることは既報のとおりである(7,10))。本研究で用いたアルミノケイ酸塩ガラスでは、Alイオンの配位数を考慮する必要がある。低アルミナ組成では[Al2O3]≦([N a2O]+[K 2O])を満たすため、すべてのAlイオンは4配位をとり、 AlO4-四面体としてガラスネットワークを構成する(29)。高アルミナ組成は[Al2O3]≦([MgO] +[CaO])を満たすものの、Al原子が高配位数を取ることが知られており、Neuvilleらによる27AlNMR測定から5配位([5]Al)、6配位([6]Al) のAl比率が定量されている(30)。NMRの定量結果によると、高配位数のAl比率(総Al原子数に対する5配位と6配位の割合の合計)は[MgO]/([MgO] +[CaO])に対して単調な変化をしておらず、格子熱伝導率との相関はみられない(Fig. 8)。以上のことから、少なくとも本研究で用いたアルミノケイ酸塩ガラス系では、Al配位数の組成に対する変化は熱伝導率において支配的な要素ではないと言うことができる。
 Fig. 8 Comparison between thermal conductivity and concentration of high coordinated Al([5]Al,[6]Al)in high Al2O3 system.
Fig. 8 Comparison between thermal conductivity and concentration of high coordinated Al([5]Al,[6]Al)in high Al2O3 system.4.3. κdiffとκpropの組成依存性
熱伝導率の組成依存性の考察を深めるために、Sørensenらと同様に各熱伝導タイプの寄与を見積もった。局在化された振動であるloconsの格子熱伝導への寄与は他の熱伝導種と比較して小さいと考えられているため(31)、フォノンに似た非局在化された伝搬モードであるpropagonsの格子熱伝導率κへの寄与 κpropは、κprop=κ-κdiffと表すことができる。Fig. 9にMg/Ca混合系propにおけるκpropとκdiffの計算結果を示す。低アルミナ系と高アルミナ系でκdiffの値に大きな差はみられないが、κpropの組成依存性には明確な違いがみられる。MgOを多く含んだ熱伝導率の高い領域(CaO/(MgO+CaO)=0〜0.4)で、熱伝導率におけるpropagonsの寄与κpropが大きいことから、高アルミナ系と低アルミナ系にみられた熱伝導率κの組成依存性の違いは、各組成系で支配的な熱伝導モードの違い(propagonsの寄与度の違い)に由来していると推察できる。
 Fig. 9 Contribution of diffusons and propagons. Dash lines represent linear fit. Solid lines represent the apparent relations.
Fig. 9 Contribution of diffusons and propagons. Dash lines represent linear fit. Solid lines represent the apparent relations.Propagonsの寄与が大きくなるガラスの組成的または構造的要因は未だ不透明である。伝搬モードであるpropagonsの寄与が大きくなる(≒伝搬モードが散乱されにくくなる)ためには、ガラスネットワークが発達していて共有結合性が高く、イオン充填率の高い構造が有利だと想定されるが、先に述べたように格子熱伝導率はイオン充填率だけでは表すことができない。また、非架橋酸素周辺の構造が熱振動を散逸させている要因だとすると、非架橋酸素に配位している修飾カチオンの数や種類によって散乱しやすさに変化が生じると予想されるが、大きな混合アルカリ土類効果は観測されていない。修飾カチオンの位置や配位数は組成によって変化することが分かっているが(32)、現状、議論に十分な研究がなされていない。
4.4. 計算熱伝導率κcalと熱伝導因子の関係
稲葉らの熱伝導率推定式(9)ではフォノンの伝搬を仮定しているため、多くの組成系で計算値と実測値は良い一致を示すものの、シリケート系ガラス、特に高熱伝導率領域において計算値と実測値との間に乖離がみられた。計算値の乖離が熱伝導モードの細分κdiffを定義しているかどうかに起因しているとすると、この乖離が格子熱伝導率κに対するκdiffの寄与がガラス組成により異なるためと考えることもできる。そこで、様々なガラス組成系について議論をするために、Fig. 7と同様に、Fig. 10には横軸を平均音速として実測した熱伝導率κ、および計算されたκdiff、κpropを示す。ここでは、本研究に用いた組成系に加えて、アルカリ混合系Na2O-Cs2O-SiO2系(10)及びSiO2ガラスの値(9)をプロットしている。平均音速に対して熱伝導率κは組成系に依らず増大傾向を示しており、イオン充填率と乖離エネルギーによって成り立つ稲葉らの推定式が成立することに対応している。ただし、組成系が異なるアルカリシリケート系やSiO2ガラスは本研究で用いたアルカリ―アルカリ土類アルミノシリケート系とは離れたところにプロットされる。熱伝導率推定式による計算値と実測値との差Δκ=κ-κcalをκpropの値に対してプロットすると、Fig. 11のような傾向が得られる。シンプルなプロットであるが、両者の間には強い相関がみられた。特に注目すべきは、平均音速が異なるが熱伝導率кの値が近いSiO2(υs =4202[m/s]、κ=1.47[W/(m・K)])とHA-25Mg(υs=4501[m/s]、κ=1.41[W/(m・K)])が同一直線上にプロットされていることである。この線形関係から、熱伝導率の推定式において実測値との差異が生じてしまう原因はpropagonsの寄与が推定式に正確に反映されていないためであると考えられる。すなわち、propagonsの伝搬とガラス組成・構造との関係性を理解することで、ガラスの熱伝導率の予測精度を向上させることができると言える。
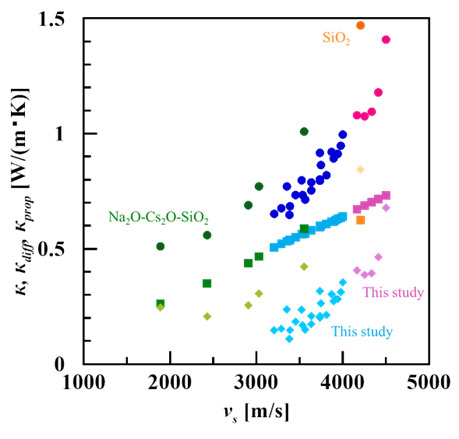 Fig. 10 Thermal conductivity of various glasses (circle:κ , square:κ diff, rhombus:κprop). The values of Na2OCs2O-SiO2 system(green) refers to reference(10). The values of SiO2 refers to reference(9).
Fig. 10 Thermal conductivity of various glasses (circle:κ , square:κ diff, rhombus:κprop). The values of Na2OCs2O-SiO2 system(green) refers to reference(10). The values of SiO2 refers to reference(9).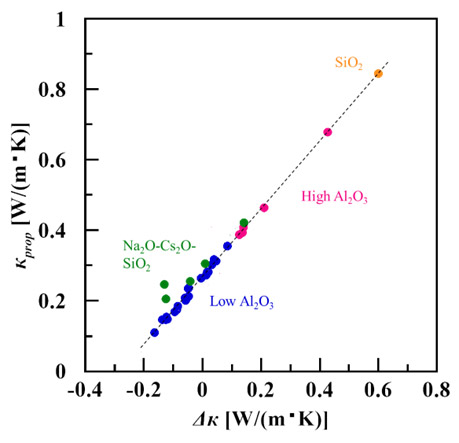 Fig. 11 Correlation between Δκ(=κ-κcal )and calculated κprop.
Fig. 11 Correlation between Δκ(=κ-κcal )and calculated κprop.5. 総括
本研究では、2種類の系統的なアルカリ土類アルミノシリケートガラス組成系について、室温における格子熱伝導率を評価した。比較的熱伝導率の低い低アルミナ系ではアルカリ土類の置換率に対して熱伝導率は線形に変化したが、熱伝導率の高い高アルミナ系では非線形な組成応答が確認された。熱伝導率に対する拡散モードの寄与を計算した結果、この非線形な偏差は混合アルカリ土類効果を主要因とするものではなく、高熱伝導率ガラス特有の挙動であることが分かった。高熱伝導率を示すガラスでは伝搬モードκpropの寄与が大きい傾向にあり、これが熱伝導率の推定値と実測値との乖離の要因であることが示唆された。現在のところ、熱伝導モードの変化とガラス構造との対応を理解することができていないが、その理解を深めることがガラスの熱伝導率の予測精度を向上させるために重要である。
謝辞
本研究にあたり、長岡技術科学大学よりインターン実習で来られた板谷梨世氏と牧和敬氏には、熱伝導率のデータ収集および実験結果の考察に多大なご協力を賜りました。ここに深く感謝の意を表します。
参考文献
- Toberer, Eric S., Lauryn L. Baranowski, and Chris Dames. “Advances in thermal conductivity.” Annu. Rev. Mater. Res. 42.1(2012) : 179-209.
- Kang, Joon Sang, et al. “Experimental observation of high thermal conductivity in boron arsenide.” Science 361.6402(2018) : 575-578.
- Mizuno, Hideyuki, Stefano Mossa, and Jean-Louis Barrat. “Beating the amorphous limit in thermal conductivity by superlattices design.” Scientific reports 5.1(2015) : 14116.
- Landry, E. S., M. I. Hussein, and A. J. H. McGaughey. “Complex superlattice unit cell designs for reduced thermal conductivity.” Phys. Rev. B Condens. Matter77.18(2008) : 184302.
- Grasso, Salvatore, et al. “Ultra low thermal conductivity of disordered layered p-type bismuth telluride.” J. Mater. Chem. C 1.12(2013) : 2362-2367.
- Kittel, Charles. “Interpretation of the thermal conductivity of glasses.” Phys. Rev. 75.6(1949) : 972.
- 松岡純.“無機ガラスの熱伝導特性.”熱測定39.3(2012) : 106.111.
- Terakado, Nobuaki, et al. “Transparent glass-ceramics for thermal management application: achievement of optical transparency and high thermal conductivity.” RSC advances 10.38(2020) : 22352-22360.
- 稲葉誠二,小田周平,森永健次.“酸化物ガラスの熱拡散率,比熱および熱伝導率の推定式.”日本金属学会誌65.8(2001) : 680.687.
- Hiroshima, Y., et al. “Thermal conductivity of mixed alkali silicate glasses at low temperature.” J. Non-Cryst. Solids354.2-9(2008) : 341-344.
- 松岡純.“ガラスの熱伝導率の組成依存性.” New glass 27(2012) : 20-23.
- Sørensen, S.ren S., et al. “Boron anomaly in the thermal conductivity of lithium borate glasses.” Phys. Rev. Mater. 3.7(2019) : 075601.
- Rodriguez, Carmen P., et al. “Thermal properties of simulated Hanford waste glasses.” J. Am. Ceram. Soc. 100.6(2017) : 2533-2542.
- Allen, Philip B., and Joseph L. Feldman. “Thermal conductivity of glasses: Theory and application to amorphous Si.” Phys. Rev. Lett. 62.6(1989) : 645.
- Allen, Philip B., et al. “Diffusons, locons and propagons: Character of atomic vibrations in amorphous Si.” Philos. Mag. B. 79.11-12(1999) : 1715-1731.
- Agne, Matthias T., Riley Hanus, and G. Jeffrey Snyder. “Minimum thermal conductivity in the context of diffuson-mediated thermal transport.” Energy Environ. Sci. 11.3(2018) : 609-616.
- Sørensen, S.ren S., et al. “Heat conduction in oxide glasses: Balancing diffusons and propagons by network rigidity.” Appl. Phys. Lett. 117.3(2020) .
- Sørensen, S.ren S., et al. “Thermal conductivity of densified borosilicate glasses.” J. Non-Cryst. Solids 557(2021) : 120644.
- Makishima, Akio, and John D. Mackenzie. “Direct calculation of Young’s moidulus of glass.” J. Non-Cryst. Solids 12.1(1973) : 35-45.
- Cahill, David G., Susan K. Watson, and Robert O. Pohl. “Lower limit to the thermal conductivity of disordered crystals.” Phys. Rev. B 46.10(1992) : 6131.
- Feldman, Joseph L., et al. “Thermal conductivity and localization in glasses: Numerical study of a model of amorphous silicon.” Phys. Rev. B 48.17(1993) : 12589.
- Kjeldsen, Jonas, et al. “Mixed alkaline earth effect in sodium aluminosilicate glasses.” J. Non-Cryst. Solids 369(2013) : 61-68.
- Fluegel, Alexander. “Glass viscosity calculation based on a global statistical modelling approach.” Glass Technol..Eur. J. GlassSci. Technol. PartA48.1(2007) : 13-30.
- Neuville, Daniel R., and Pascal Richet. “Viscosity and mixing in molten(Ca, Mg) pyroxenes and garnets.” Geoch. Cosm. Act. 55.4(1991) : 1011-1019.
- Hayes, D. J., S. N. Rea, and A. R. Hilton. “Thermal conductivity of infrared transparent chalcogenide glasses.” J. Am. Ceram. Soc. 58.3‐4(1975) : 135-137.
- Henderson, G. S. “A Si K-edge EXAFS/XANES study of sodium silicate glasses.” J . Non -Cryst . Solids 183.1-2(1995) : 43-50.
- Greaves, G. N., et al. “Local structure of silicate glasses.” Nature 293.5834(1981) : 611-616.
- McKeown, D. A., G. A. Waychunas, and G. E. Brown Jr. “EXAFS study of the coordination environment of aluminum in a series of silica-rich glasses and selected minerals within the Na2O-Al2O3-SiO2 system.” J. Non-Cryst. Solids 74.2-3(1985) : 349-371.
- Mysen, B.O. “Structure and Properties of Silicate Melts.”(1988) Elsevier, Amsterdam.
- Neuville, Daniel R., et al. “Structure of Mg-and Mg/Ca aluminosilicate glasses: 27Al NMR and Raman spectroscopy investigations.” Am . Mineral . 93.11-12(2008) : 1721-1731.
- Lv, Wei, and Asegun Henry. “Non-negligible contributions to thermal conductivity from localized modes in amorphous silicon dioxide.” Scientific reports6.1(2016) : 35720.
- Cormier, L., and D. R. Neuville. “Ca and Na environments in Na2O.CaO.Al2O3.SiO2 glasses: influence of cation mixing and cation-network interactions.” Chem. Geol. 213.1-3(2004) : 103-113.