*AGC株式会社 先端基盤研究所（takeshi.kida@agc.com）
**株式会社NTTデータ（Takashi.Yazane@nttdata.com）

　近年、量子コンピュータ活用の期待が急速に高まっている。ゲート方式については、実課題を解くにはまだキュービット数が不足しており、フィデリティーの低さも課題となっている。一方、量子アニーリングを含めたイジングマシンにおいては、実課題が解けるビット数が利用可能となりつつあり、数年以内に実運用ができると期待されている。このような期待は、「イジングマシンにより、組合せ最適化問題の厳密解を、古典コンピュータよりも高速に計算できる」という前提に基づいているが、実際のパフォーマンスは最適化問題の種類によって異なるため、用途に応じた検証が必要である。そこで本研究では、イジングマシンを「板取り問題」と呼ばれる組合せ最適化問題に適用し、最適解を得るためのアルゴリズムを考案した。板取り問題とは、母材と呼ばれる大きなガラスから窓サイズの製品ガラスを無駄なく切り出す組合せ最適化問題であり、ガラス産業において歩留まりに直結する重要な課題である。本課題は、製品枚数が多くなると古典コンピュータでは多項式時間で解くことができなくなるNP困難問題 （Non-deterministic P: 非決定的多項式時間）として知られており、イジングマシンで高速化することができれば大きなメリットが期待される。

　本研究では、板取問題のヒューリスティクスな方法としてよく利用されるNext-Fit DecreasingHeight （NFDH） 法をベースに定式化を行い、D-Waveと東芝Simulated Bifurcation Machineの2つの実機を用いて、現時点での量子アニーリングマシンと古典分岐マシンの性能を比較した。また、NFDH法では表現できない製品配置について、イジングマシンを繰り返し使うアルゴリズムを提案し、より複雑な問題にも対応できることを確認した。

Expectations are increasing for applications of quantum computers. For the gate method,overcoming the shortage of qubits and low fidelity remains a big obstacle to solving practical optimization problems. Conversely, Ising machines, including quantum annealing, are expected to enter practical use within a few years because they make available numerous bits. This expectation is based on the assumption that Ising machines can exactly solve any combinatorial optimization problem faster than a classical computer. However, the performance of a classical computer and of the Ising machine depends on the type of problem. The present study develops an Ising-machine algorithm and applies it to solve the"cutting stock problem"（CSP）, which is a combinatorial optimization problem to cut out window-sized products from larger base glass plates so as to minimize glass loss. The CSP is one of the most important optimization problems for the glass industry because of its direct contribution to production yield. Given that this problem is NP hard and, with increasing problem size, cannot be solved in polynomial time, an accelerated solution via the Ising machine promises a significant benefit. In this study, the CSP is formulated by using the next-fit decreasing height （NFDH） method, which is commonly used as a heuristic to solve the problem. The algorithm is tested on two real machines: D-Wave and the Toshiba simulated bifurcation machine. In addition, we propose a method involving the repeated running of the proposed algorithm to overcome the limitation of the NFDH-based formulation. This algorithm is also examined by using the Toshiba simulated bifurcation machine and the Ising simulator.

1. 緒言

　ガラスや鉄鋼、木材などの素材加工業では、板状の母材を実際の製品サイズ・形状に切り出す工程がある。与えられた数量のアイテムをできるだけ少ない母材から切り出す問題は「板取り問題」と呼ばれ、NP 困難であることが知られている。

　本研究では、ガラス加工において重視されるギロチンカット制約とn-stage 制約を考慮した板取り問題を取り扱う。ギロチンカット制約とは、材料の端から端までを途中で曲がらずに一直線に裁断する切断方式を表す。加えて、n 回のギロチンカットによって、アイテムを切り出せるとき、n-stage制約を満たすと表現する。これらを考慮した研究例は数多く報告されているが、計算時間の制限から構築型の手法や局所探索法などの近似解法を用いることが一般的である^［1］。一方で、整数計画による厳密解の求解も研究されている^［2］。最近の研究では、無限ステージのギロチンカット制約を満たす板取り問題を定式化し、分枝限定法によって厳密解を得る手法も提案されている^［3,4］。ただ、この手法では問題規模が大きくなると求解に多大な時間を要する。

　これらの先行研究は全て古典コンピュータのためのアルゴリズムである。一方、次世代の最適化計算機として量子アニーリングなどのイジングマシンが注目されている。イジングマシンによって大規模な最適化問題を高速に解けることが期待されるが、現段階では求解の規模や精度に限界があることが知られている^［5］。板取り問題をイジングモデルで解いている先行研究は存在するが、ギロチンカット制約を考慮しない手法が提案されている^［6］。本研究では、量子アニーリングに基づいたD-Wave 2000Q（QA）^［7］と古典力学の分岐現象に基づいた東芝Simulated Bifurcation Machine（SBM）^［8］を用いて、ギロチンカット制約を考慮した板取り問題の求解を試み、それぞれの性能を比較した。

2. 実験方法

2.1. 実験課題

　板取り問題は、母材の条件からCutting Stock 問題とStrip Packing 問題の2 種類に分類できる。ガラス加工業界では、あらかじめ一定のサイズに切断した母材に製品を割り当てていくCutting Stock 方式が一般的である。しかし、母材ごとに変数が必要になるため、これを現在のイジングマシンに実装するのは困難である。そこで本研究では、高さ無限大の1 枚の母材からアイテムを切り出すStrip Packing 問題について定式化を行った。先に述べたギロチンカット制約を満たすべく、Next-Fit Decreasing Height（NFDH）法^［9］を参考に定式化を行った。

2.2. NFDH法

　従来のヒューリスティックなNFDH 法は、アイテム（製品）を配置する順番をあらかじめ決め、幅W、高さHの母材の左下を原点として、順番にアイテムiを配置していく。アイテムiの幅をw_i、高さをh_iとする（Fig. 1）。

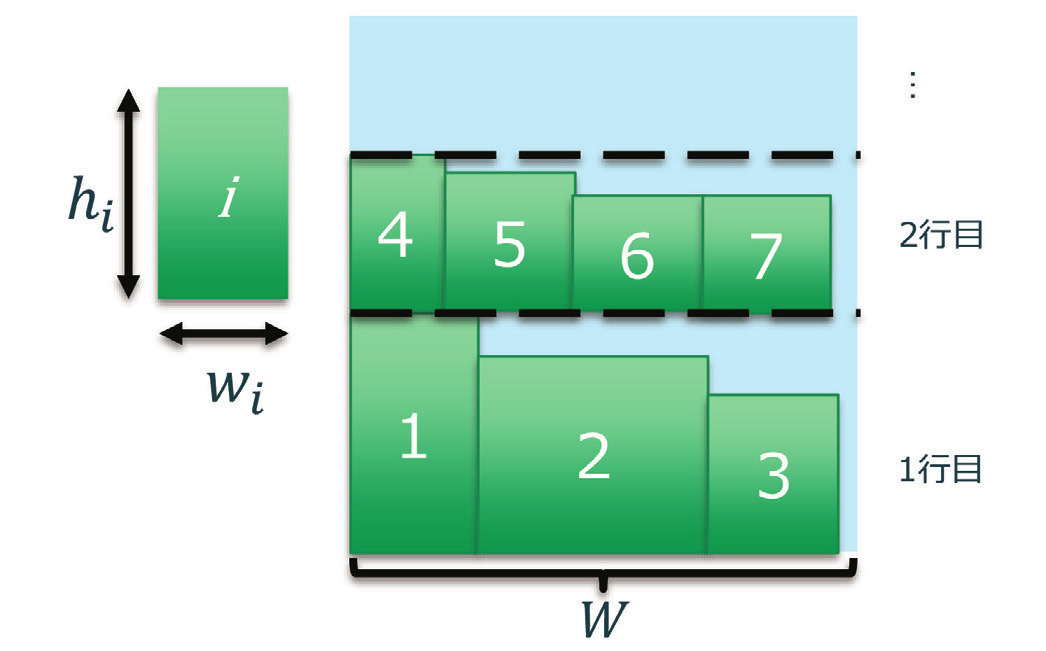Fig. 1 An example of plate arrangement with NFDH method

初めに配置したアイテム（w₁, h₁）の高さを基準にして、次に配置するアイテム（w₂, h₂）に対して、

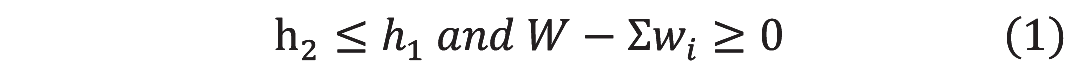
が成立するなら、隣接するように配置する。（1）式が成り立たない場合は、資材（w₂, h₂）は座標（0, h₁）に配置する。

2.3. 定式化

　イジングマシンのための定式化を以下に示す。本研究では、アイテムを置けない空白部分（ロス）を最小化する目的関数を以下のように設定する。

・目的関数

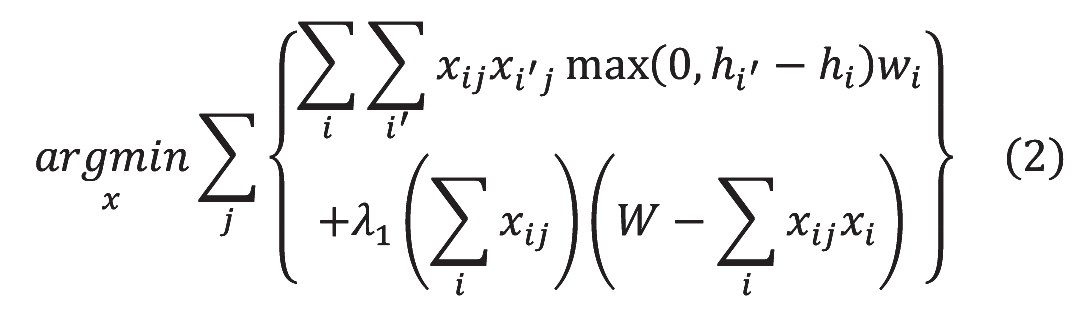
ここで、x_ijは決定変数であり以下のように定義される。

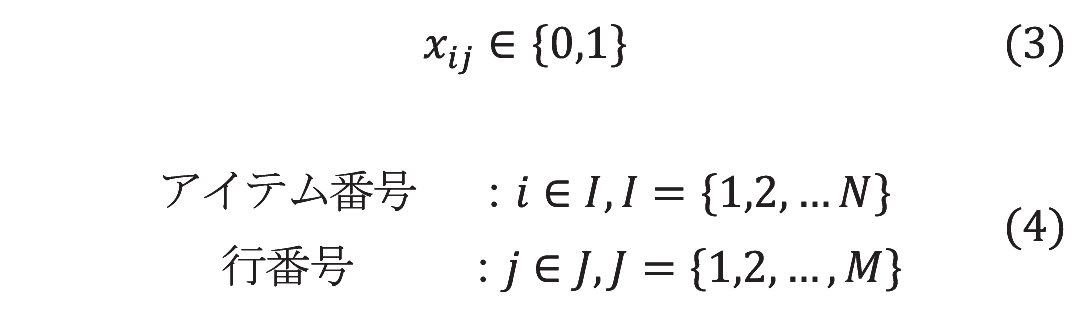
　従来のNFDH 法では、同じ列にある左隣に配置されたアイテムの高さの差分がロスとなる。そのロスの合計を（2）式の第一項で表現している。イジングマシンではどのアイテムが右隣に来るかは事前にわかないため、ロスの算出は配置したアイテムの左側にあるすべてのアイテムとのロスを総和する形とした。

　（2）式の第2項は、各列における幅方向のロスの合計を示しており、ロスが大きくなるほど目的関数が大きくなる。第1項は面積を合計しているのに対して、第2項は寸法を合計しており、扱っている次元が違うので、重みを第二項にかけることで、それぞれの項の目的関数への寄与を調整している。

　また、板取り問題では、定式化すべき制約が2 つある。一つは、各アイテムは1 回だけしか使用してはいけないという制約であり、（5）式で示す。もう一つは、アイテムが母材の幅方向を超えて、配置してはいけない制約であり、（6）式で示す。

・制約条件

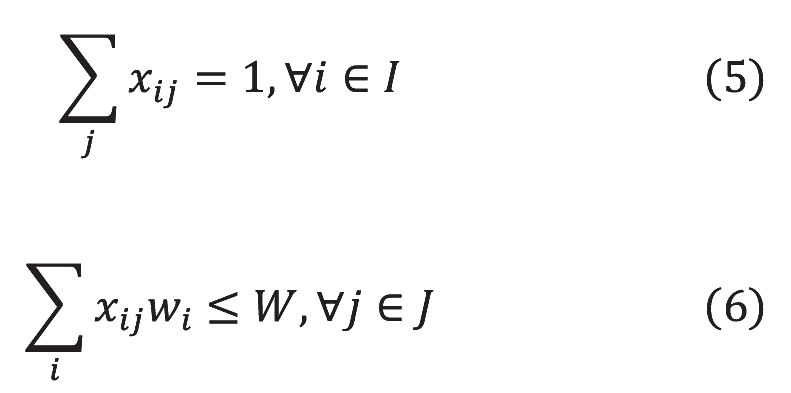
3. イジングマシンによる数値実験

3.1. 問題概要

　本実験では、母材4枚からなるFig. 2の問題を対象とした。図の配置は解の一例である。

問題のスケールが上がることによって求解精度がどのように変化するかを観察するために、Table. 1のように、母材4枚から、2枚～4枚を選んで縦に積み重ねることで、Strip Packing問題として扱っている。組み合わせパターンNo. 1のイメージをFig. 3に示す。また、問題番号が大きくなるにつれて、問題サイズが大きくなるようにした。

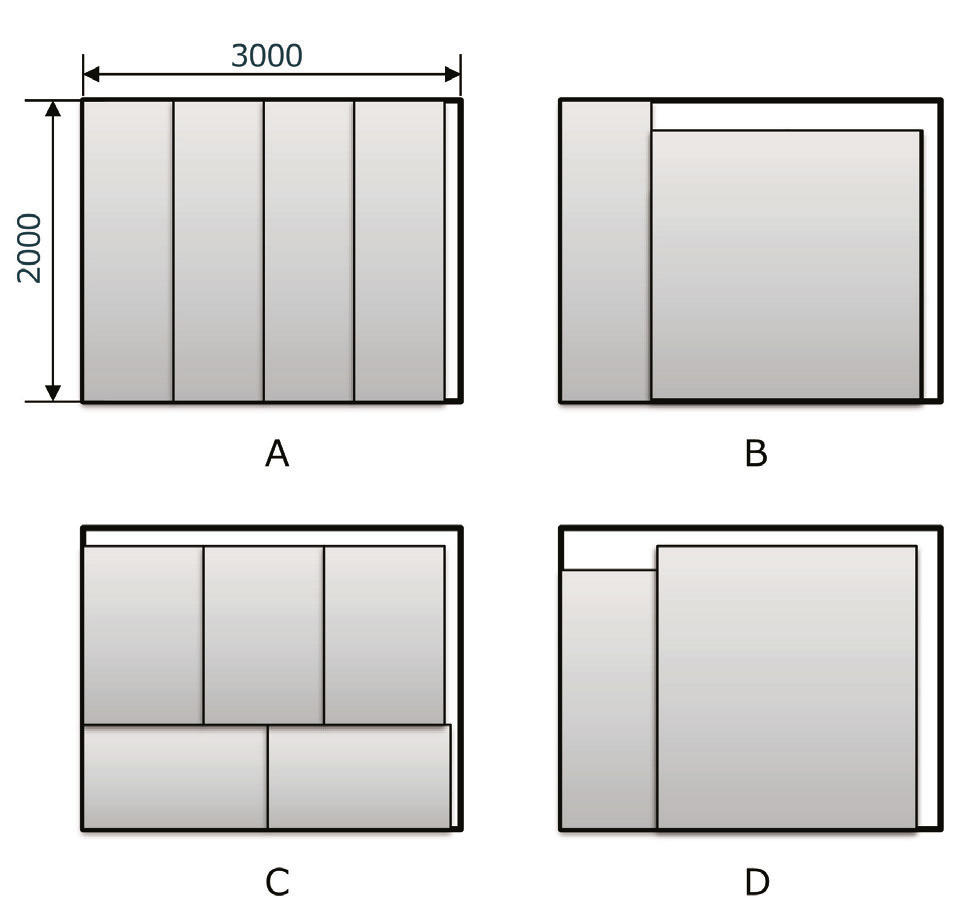Fig. 2 Patterns of sample arrangements for the first problem.

Table. 1 Combination pattern

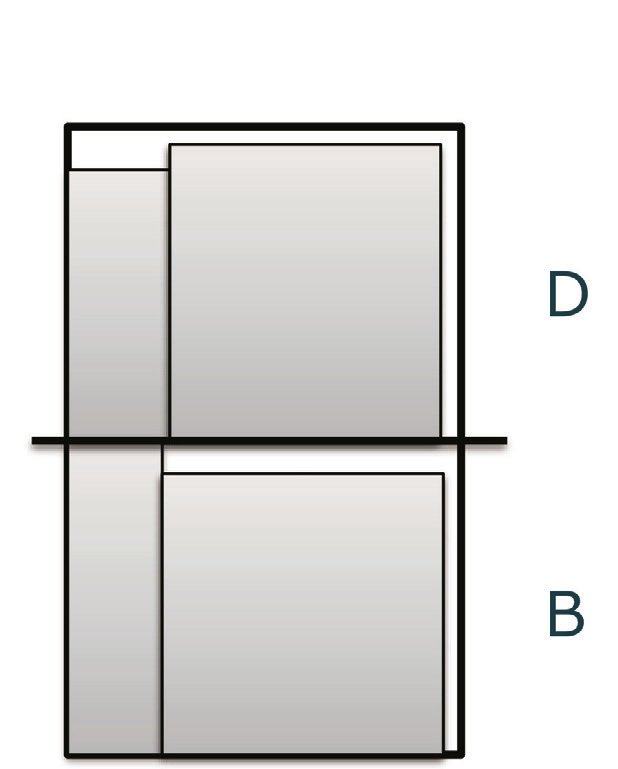Fig. 3 An example of combination pattern.

3.2. 実験方法

　イジングマシンで問題を解くために、（2）～（6）式をQuadratic Unconstrained Binary Optimization（QUBO）へ変換し、QAとSBMで計算した。QUBOへの変換にはPyQUBO^［10］を用いた。イジングマシンは、一度の計算で最適解を返す保証がないため、複数回計算させて良い解を抜き出した。

　本実験では、前節で示した11種類の問題をそれぞれ1000回解いたときに、実行可能解と最適解が得られた回数を計測した。また、問題の規模が増大したときの解の変化を観察した。

3.3. 結果

　QAとSBMの結果を比較するために、Fig. 4に並べて示す。各問題において、Fig. 2と同等の詰込みができていれば正解と呼び、制約は守っているがFig. 2のようにコンパクトに詰込みができなかった場合の解を実行可能解と呼ぶ。QAで数値実験を行ったところ、No. 7までの問題では正解を得られたが、No. 8以降の問題では実行可能解すら得られなかった。一方、SBMは全ての問題で実行可能解が得られ、No. 11以外は正解も得られた。No. 2と7を除くと、過半数以上が実行可能解を得られており、正解を得られている数も比較的多いことがわかる。板取問題を今回の定式で解くにあたり、SBMでも比較的小規模な問題については十分に求解可能である。

　問題Noが大きくなるについて、使用する量子ビットが増える。QAにおいて、使用する量子ビットが増えるにつれて、制約が満たせない解が増えてくる。QAはノイズに弱いことが知られているが、使用する量子ビットが増えることで、ノイズによるビット情報を正しく持てないものが増え、最終出力時に制約違反を起こしている解を得ていると考えられる。一方、SBMにおいては、使用する量子ビットが増えていても制約違反の解が多くなるわけではなく、その代わり実行可能解を多く得る傾向が見られる。量子インスパイアマシンであるSBMはノイズによる量子ビットの反転が起こることはほとんどないことを示していると共に、ローカルミニマムの解にトラップしやすことを特徴付けていると考えられる。

　今回の定式化では、決定変数のすべての組み合わせを考慮する必要がある全結合問題になっている。QAはハードの制約上、全結合ではなく、疎結合となっている。そのため、全結合を想定している問題を解くためには、疎結合を全結合に模擬させるためのパラメータを設定する必要があるのだが、この設定はかなり難しい。一方、SBMは全結合が想定されたハード使用となっているので、全結合問題を解く上で特殊なパラメータを設定する必要はなく、ユーザーとしては、全結合問題は全結合マシンに解かせる方が良い解を得やすいと考えられる。ゆえに、実用性を考えると、現時点ではノイズに弱く疎結合しか選択肢がない量子アニーリングに固執せず、量子インスパイアマシンの活用が有用である。

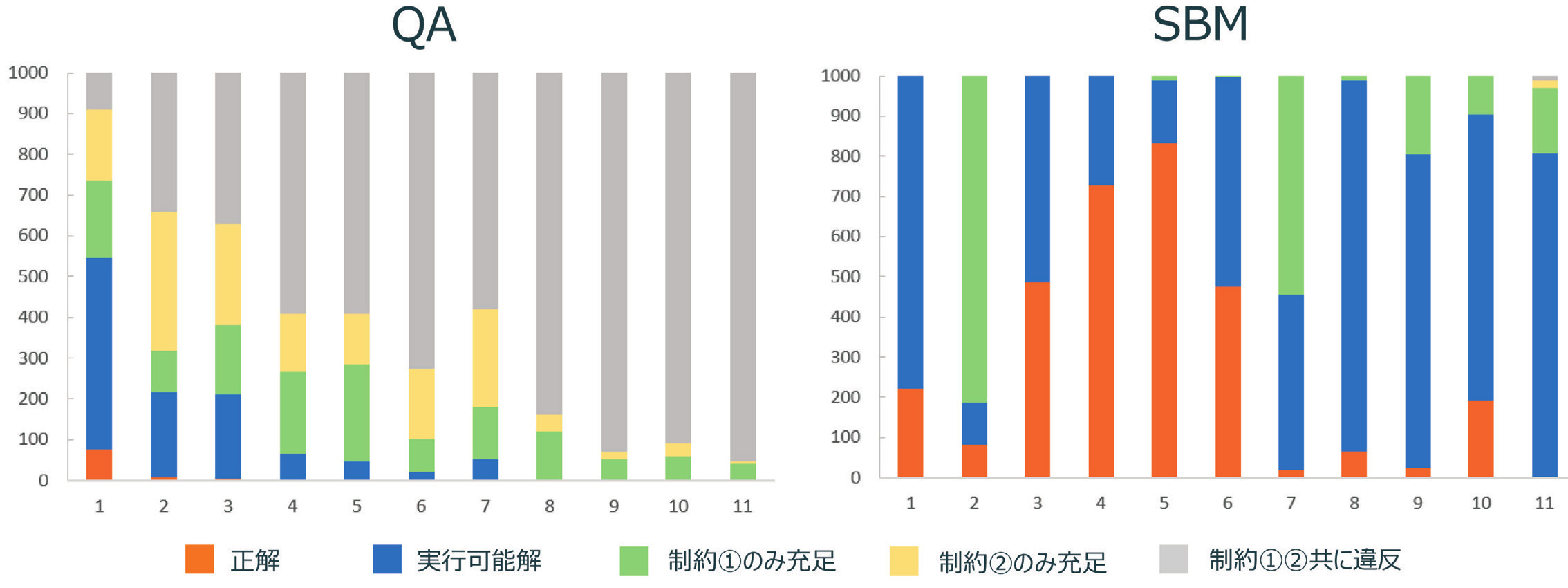Fig. 4 A comparison between D-wave and Toshiba SBM

4. n-stageへの応用

4.1. アルゴリズム概要

　3章にてNFDH法を参考に定式化した方法では、各行で幅方向にアイテムを並べていた。そのため、3-stage 制約以下の制約は満たせるが、4-stage以上の配置には対応ができない。そこで、提案した定式化を利用して、4-stage以上を実現できないか検討した。検討したアルゴリズムは、以下の通りである。Fig. 5に概要図を記載した。

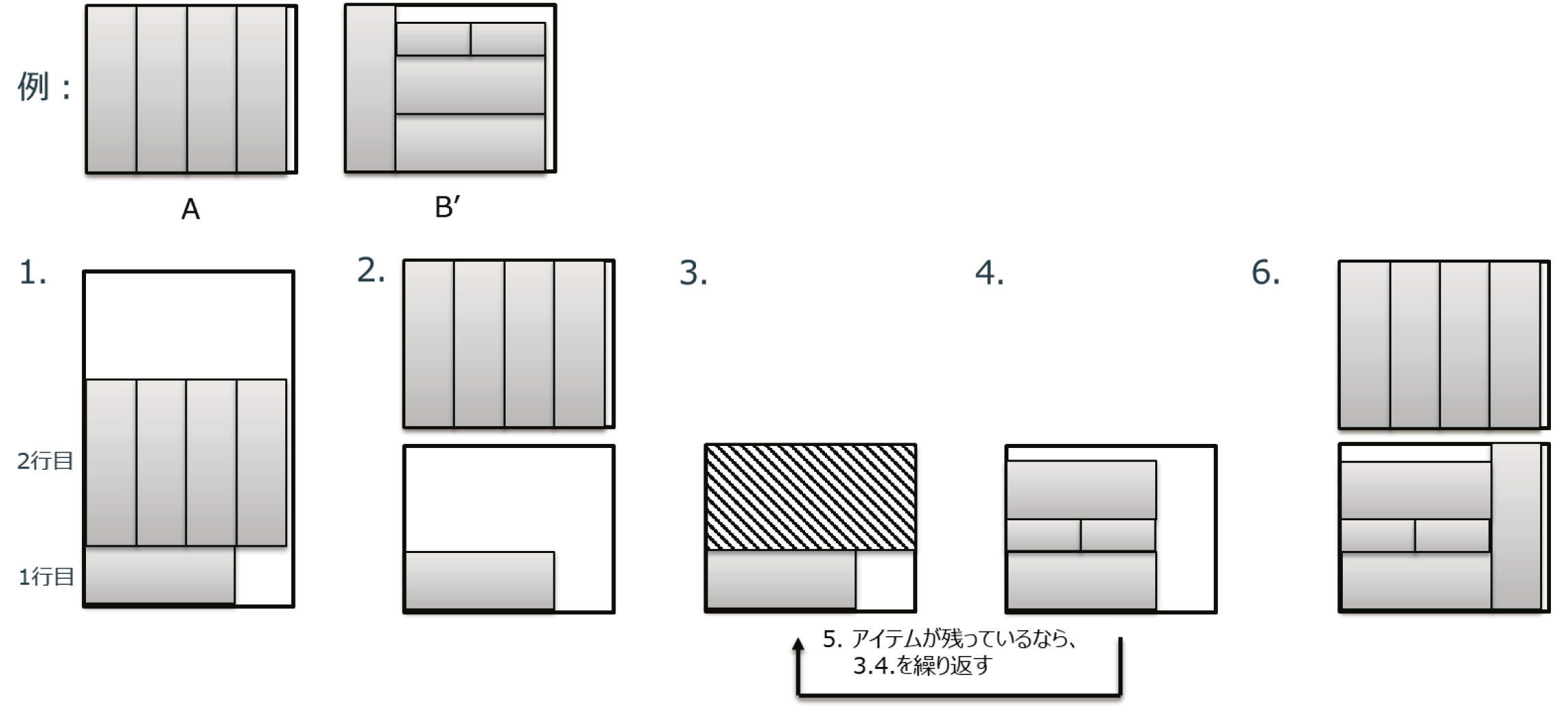Fig. 5 A schematic flow of algorithm for n-stage problem.

　上記のstep.1と3でイジングモデルを使っており、その他の部分はCPUでの処理を行った、イジングモデルとCPUのハイブリッドアルゴリズムである。

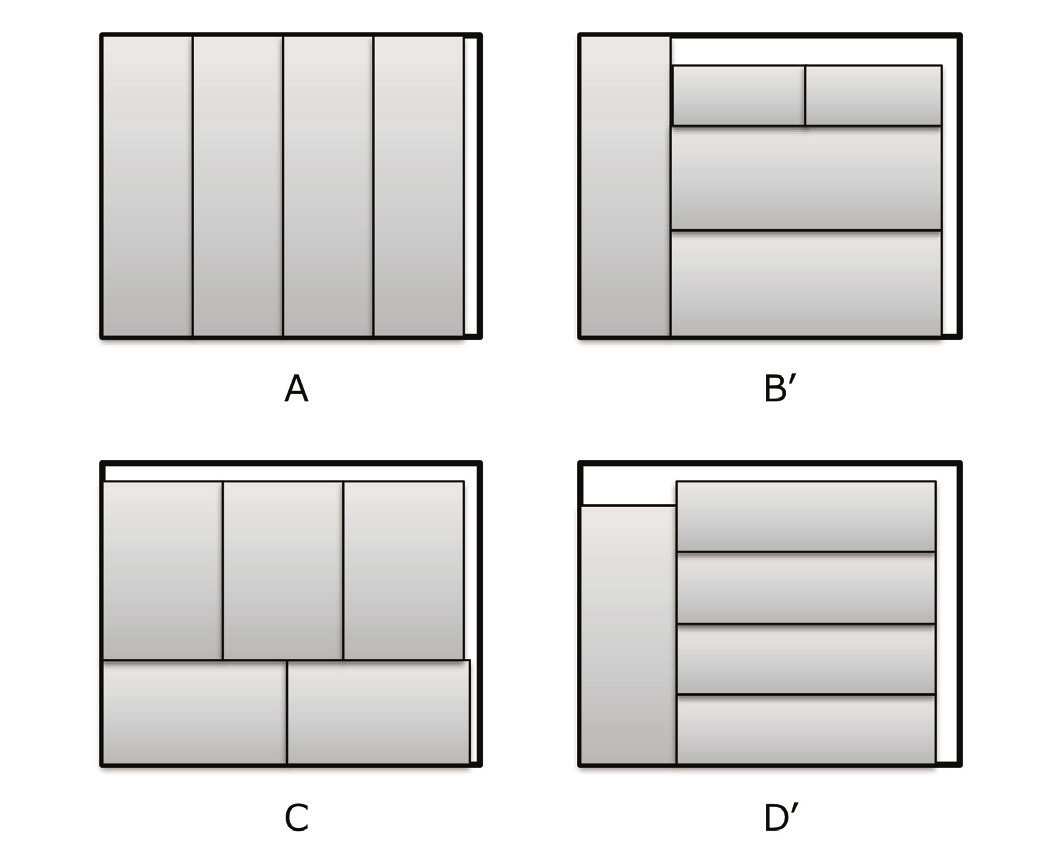Fig. 6 Glass cutting with multiple pileup

　本章で扱う問題と解をFig. 6に示す。Fig. 2のパターンB、Dそれぞれにおいて、右側に配置されていた大きい製品を、今回のために複数枚に分割し、パターンB’とD’とした。ここでも問題スケールによって解の精度の変化を調べるために、Tabel. 1のように問題規模を変化させながら、実験する。

4.2. 実験方法

　今回の多段化実験では、まず初めに、本アルゴリズムによって想定した解が得られることを確認するためにSimulated Annealing（SA）で解いてみた。SAでは、11種類の問題を50回解き、解答例と同等の精度かそうでないかを判定した。加えて、SBMでも同様に11種類の問題を50回解き、解答例と同等の精度かそうでないかを判定した。また、両者の計算時間についても違いがあるのか評価した。

4.3. 結果

　Fig. 7の上段にSAで計算した結果を示す。No. 3、5、6においては、ほぼすべての計算で正解が得られていることがわかる。しかし、同じ母材2枚の問題でもNo. 1、2、4においては、正解である母材2枚で収まる解があまり得られていないことがわかる。No. 1、2、4とNo. 3、5、6の違いはパターンB’が含まれているかどうかである。Fig. 2とFig. 6を比較すると容易にわかるが、第3章で用いたFig. 2では、Fig. 6のパターンB’とD’にある一部のアイテムを結合して一つの板としていた。この章で用いているFig. 6において、パターンD’は幅方向の大半を占める板が4枚積み重なっているのに対して、パターンB’は2枚の小さな板が存在している。小さい板は他の大きいものに比べて、小さい隙間にも配置ができるため、思わぬところで使用されてしまうと、残りの大きい板がおけるスペースがなくなり、母材2枚で収まらないケースが発生し、正解が得られない回答が返ってくる。No. 7以降の課題では、パターンB’とD’の有無やアイテム数・必要な行数といった問題の難しさに比例して、理想解が得られる比率が下がるような結果が得られた。

　SBMで実験した結果をFig. 7の下段に示す。SBMでは、SAに比べて大きく正解数に違いはないが、少し多くの正解が得られている。SAの結果と比較して大きく違う点が2つ認められる。1つは、No. 2の課題において、SAではほとんど理想解が得られなかったのに対し、SBMでは全ての試行で理想解が得られている。2つ目は、No. 5の課題において、SBMの正解率がSAに比べて半分程度になっている。SAの時のように、特定の板の有無によって正解率が増減するような傾向は容易にはみられない。そのため、SBMでは、SAのように特定の板（パターンB’）があるために正解率が大きく変動しているわけではないと考えられる。

　ここで、上記の考えが事実か確かめるために、特定の板が含まれることで正解数にどのように変化するのか考える。Table. 2にパターンA~Dの有無毎に正解数を手法別にまとめた。SAでは、パターンB’を含まない問題とパターンB’を含む問題とで正解数に差が出ていることがわかる。また、パターンB’を含まない問題については、正解率に差がないことから、パターンB’を含む問題が得意的に苦手であることが分かる。

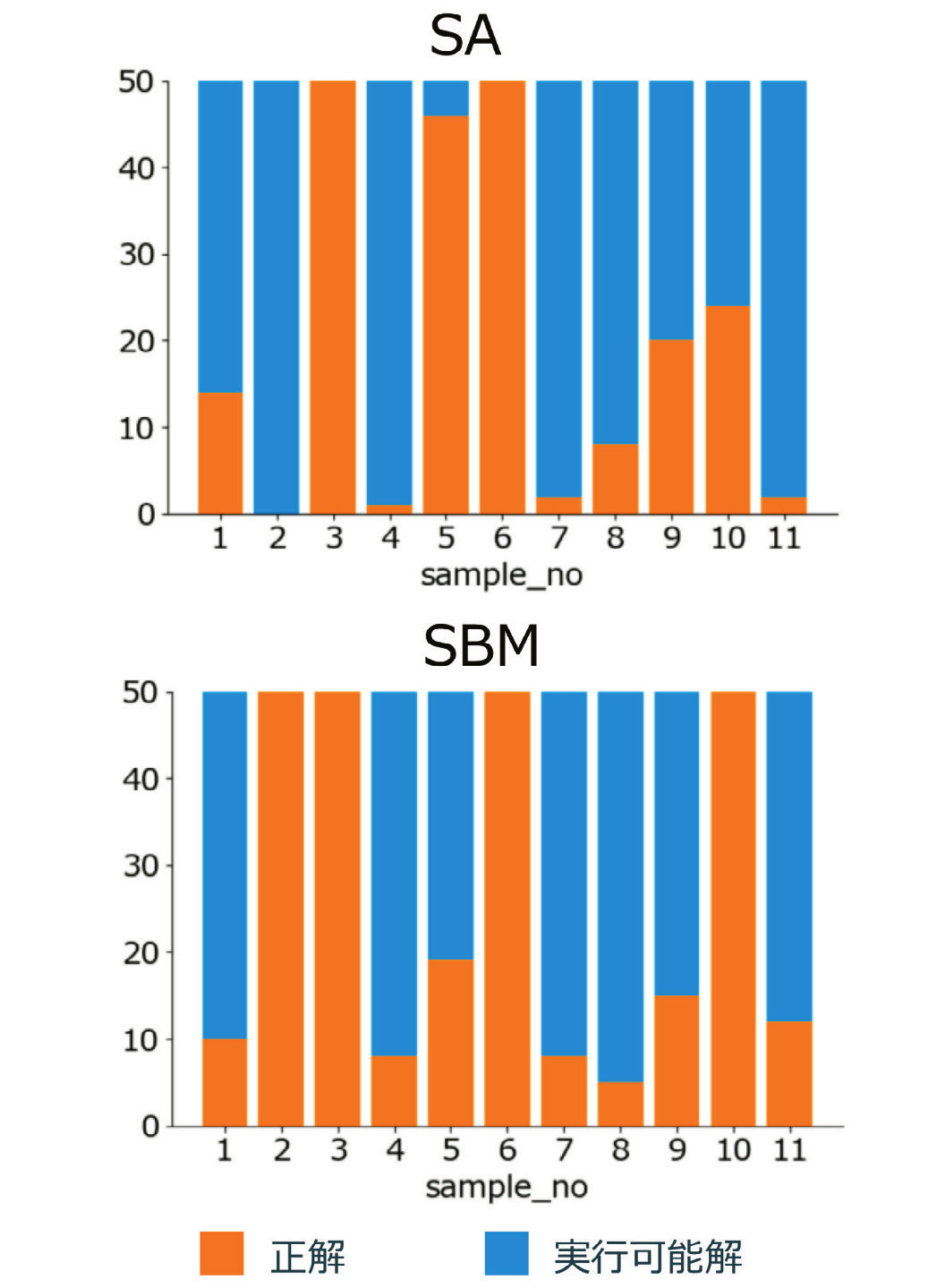Fig. 7 Ratio of correct answers to n-stage sampling problem.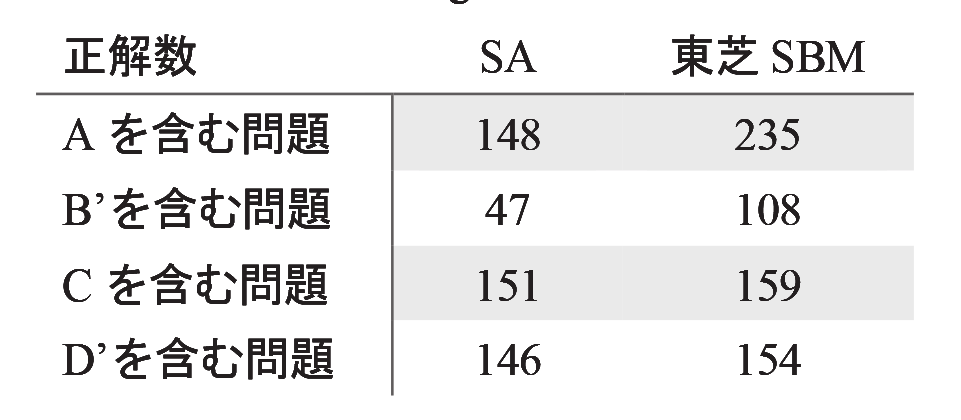

Table. 2 The number of correct answers for each plate

　一方、SBMに関してみると、SAと同様にパターンB’を含む問題は他に比べると正解数が少ない。ゆえに、今回のアルゴリズムは、パターンB’のような特定の組み合わせを苦手とする傾向がある。加えて、SAとSBMを比較すると、パターンCとD’の組み合わせを含む問題に関しては、正解数に差がないが、パターンAとB’の組み合わせに対しては、SBMの方が、正解を多く得られている。本件は、ハードウェア依存である可能性もあるため、運転パラメータを変更した時にどう変化するのか、ハードウェアに合わせて調整・観察する必要があると考えられる。

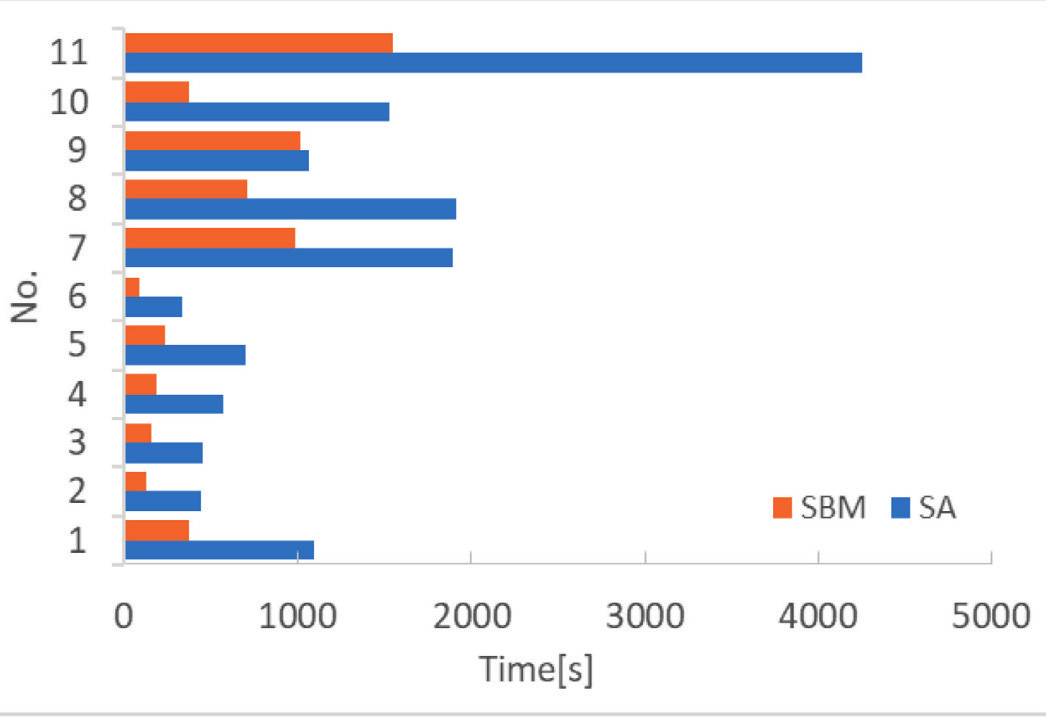Fig. 8 Calculation time

　計算時間の比較を、Fig. 8に示す。SAと比べてSBMの方が、すべての課題において短時間で計算が終了していることが分かる。実際、No. 9の課題以外では、SAの半分以下の時間で解析ができている。今回のアルゴリズムは、Fig. 5のステップ5にあるように、イジングモデルを何度も繰り返し解く必要があるため、1回の計算が早いSBMの方が、トータル時間でSAに比べてかなりの計算時間の短縮につながっていると考えられる。

5. 総括

　ギロチンカット制約とn-stage 制約を考慮した板取り題を、イジングマシンで求解する手法の検討と実装を行った。

　最初に、3-stageで切り出せるNFDH法をベースに問題をイジングモデルに定式化して実験した結果、QAに比べてSBMの求解結果の方が良好であった。

　次に、実問題は複雑な配置構造をしているため、4-stage以上にも対応する必要がある。上記で提案したNFDH法ベースのイジングモデルを繰り返し使う手法を提案し、複雑な配置も最適化できることを示した。これらの数値実験から、シミュレータのSA法に比べて、実機のSBMの方が、求解精度と計算時間において、有利であることが確認でき、今後さらに実機の活用が期待できる。

　現時点ではビット数の制限によって実現していないが、今後はアイテムの90 度回転を考慮したCuttingStock問題の解法についても検討を行いたい。

参考文献

1. E.K.Burke, G.Kendall and G.Whitewell, "A new placement heuristic for the orthogonal stock-cutting problem",Operations Research, 52, 2004, 655-671.
2. Haessler, Robert W., and Paul E. Sweeney. "Cutting stock problems and solution procedures." European Journal ofOperational Research 54.2 , 1991, 141-150.
3. A. Bekrar and I. Kacem, "An exact method for the 2Dguillotine strip packing problem," Advances in OperationsResearch , Vol. 2009, Article ID 732010, 2009.
4. F. Furini, E. Malaguti and D. Thomopulos, "Modeling twodimensional guillotine cutting problems via integer programming," INFORMS Journal on Computing , Vol. 28,Issue 4, pp. 736-751, 2016.
5. 西森秀稔, 経産省シンポジウム「次世代コンピュータが実現する革新的ビジネス」基調講演, 2019
6. Terada, Kotaro, et al. "An Ising model mapping to solve rectangle packing problem." 2018 International Symposium on VLSI Design, Automation and Test (VLSIDAT).IEEE, 2018.
7. D-Wave Technology Overview : https://www.dwavesys.com/sites/default/files/Dwave_Tech%20Overview2_F.pdf
8. Hayato Goto, Kosuke Tatsumura and Alexander R.Dixon, "Combinatorial optimization by simulating adiabatic bifurcations in nonlinear Hamiltonian systems",Science Advances 19 Apr 2019 Vol. 5, no. 4, eaav2372
9. E. G. Coffman Jr., M. R. Garey, D. S. Johnson and R. E.Targan, "Performance bounds for level-oriented twodimensional packing algorithms," SIAM Journal onComputing , Vol. 9, Issue 4, pp. 801-826, 1980.
10. PyQUBO：https://github.com/recruit-communications/pyqubo
11. 喜田, 塔ノ上, 矢実, 立川, 香月, "ギロチンカット制約を有する板取り問題へのイジングマシンの適用", 日本オペレーションズ・リサーチ学会, 2020年春季研究会, 2-F-8